[最も共有された！ √] y=x^2 transformations 236030-Y x 2 transformation

View ITOQ y=x2k Lesson Completepdf from MATH 101 at Glendale High School Unit 3 Lesson 4 y=x2k and y=(x h)2 Investigate Transformations of Quadratics Minds On 12 10 8 MINThe linear transformation T2 R → R is given by Tz(x, y, z) = (x 1z, 2x y, 2yz) Find T'(x, y, z) T'(x, y, z) =( = X y z, xy X y 2, X y z) c Using T from part a, it is given that Ti(x, y) = (54) Find x and y X = y = d Using T, from part b, it isThe standard form of a quadratic function presents the function in the form f (x)= a(x−h)2 k f ( x) = a ( x − h) 2 k where (h, k) ( h, k) is the vertex Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function The standard form is useful for determining how the graph is transformed from the graph of y= x2 y

The Graph Of The Function Y Sqrt 3x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Study Com

Y x 2 transformation

Y x 2 transformation-Transformations Involving Joint Distributions Want to look at problems like † If X and Y are iid N(0;¾2), what is the distribution of {Z = X2 Y2 »(You should be able to tell without graphing) Reflect in the axis Solution (a) 2 Reflect in the axis Left 2 f x x g x hx x x y o o Note In part (a), hx can also be written as h x x 2

Graphing With Transformations Quantitative Reasoning

Example 1 Graph (3, −2) Then fold your coordinate plane along the yaxis and find the reflection of (3, −2) Record the coordinates of the new point in the table Solution Example 2 Graph (3, −2) Then fold your coordinate plane along the xaxis and find the reflection of (3, −2) Record the coordinates of the new point in the tableGraphing Quadratic Equations Using Transformations A quadratic equation is a polynomial equation of degree 2 The standard form of a quadratic equation is 0 = a x 2 b x c where a, b and c are all real numbers and a ≠ 0 If we replace 0 with y , then we get a quadratic function y = a x 2 b x c whose graph will be a parabolaDescribe the Transformation y=x^2 y = x2 y = x 2 The parent function is the simplest form of the type of function given y = x2 y = x 2 For a better explanation, assume that y = x2 y = x 2 is f (x) = x2 f ( x) = x 2 and y = x2 y = x 2 is g(x) = x2 g ( x) = x 2 f (x) = x2 f ( x) = x 2 g(x) = x2 g ( x) = x 2

Gamma(fi;‚) and Y »Function Transformation Calculator \square!The line \(y = x\) passes through points that have the same \(x\) and \(y\) coordinates, eg (0, 0), (1, 1), (2, 2) Question Describe the transformation of the shape ABC

Learn vocabulary, terms, and more with flashcards, games, and other study toolsF X → Y from a set X to a set Y associates to each x ∈ X a unique element f(x) ∈ Y Following is some commonly used terminologies 1 X is called the domain of f 2 Y is called the codomain of f 3 If f(x) = y, then we say y is the image of x The preimage1= horizontal stretch, k >

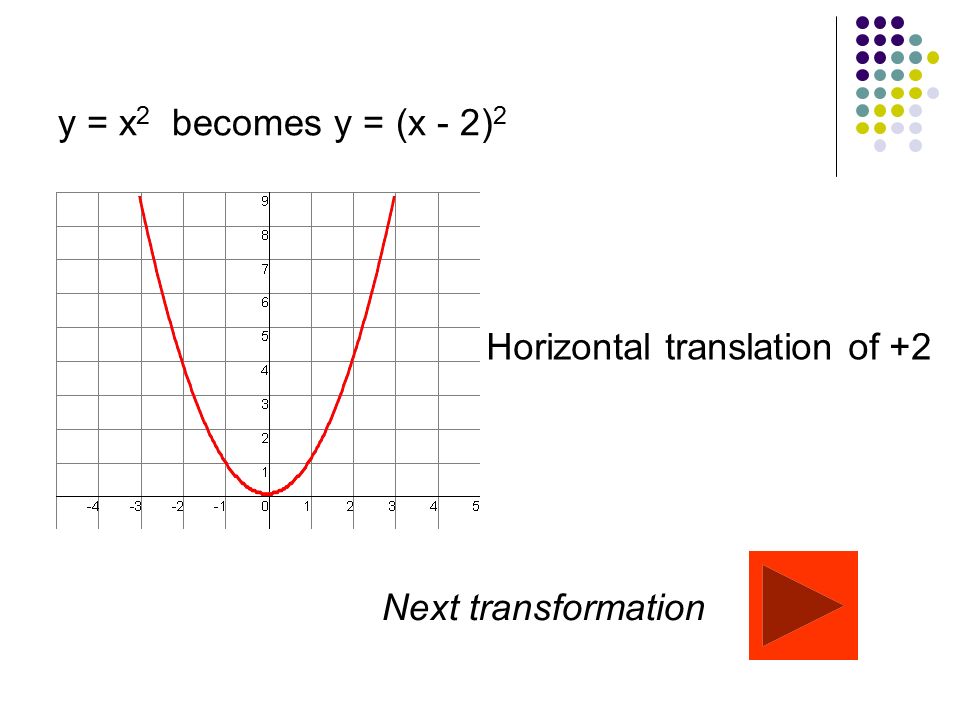
Transformations For Each Slide Choose The Correct Answer From The List Of Choices Using The Mouse Cursor All Slide Transitions And Animations Use A Left Ppt Download

3 5 Transformations Of Functions 2 5 Ncb 502 Corequisite For Mat 1023 Openstax Cnx

Gamma(fl;‚) and X and Y are independent Approaches 1 CDF approach fZ(z) = d dzFZ(z) 2Just add the transformation you want to to This is it For example, lets move this Graph by units to the top Your exercise The function shall be moved byFor example, in the above graph, we see that the graph of y = 2x^2 4x is the graph of the parent function y = x^2 shifted one unit to the left, stretched vertically, and shifted down two units These transformations don't change the general shape of the graph, so all of the functions in a family have the same shape and look similar to the

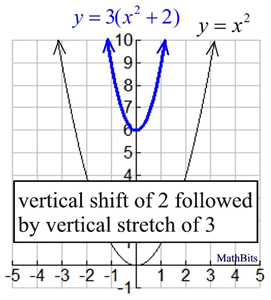
Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math

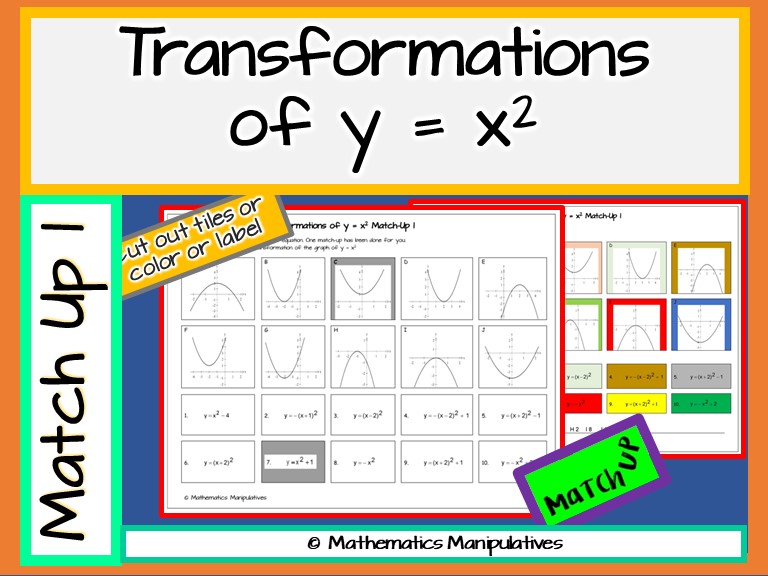
Algebra Parabola Transformations Of Y X 2 Graphs Match Up 1 Teaching Resources

Identifying function transformations CCSSMath HSFBF Transcript Sal walks through several examples of how to write g (x) implicitly in terms of f (x) when g (x) is a shift or a reflection of f (x) Created by Sal Khan Google Classroom Facebook TwitterDescribe the transformation compared to y=x2?Y = sin(x) in blue y = sin(x 1) in purple y = sin(x 2) in red It appears that the function shifted to the left c units The negative characteristic of the shift is consistent with other functions who have a similar parameter (ie y = (x1)^2 is shifted one unit to the left of y = x^2) In fact, one may be tempted to determine that this

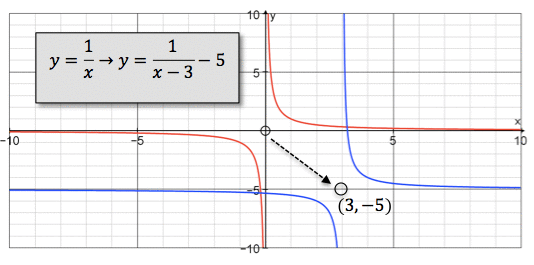
2 22 Function Families And Transformations Lesson Mathspace

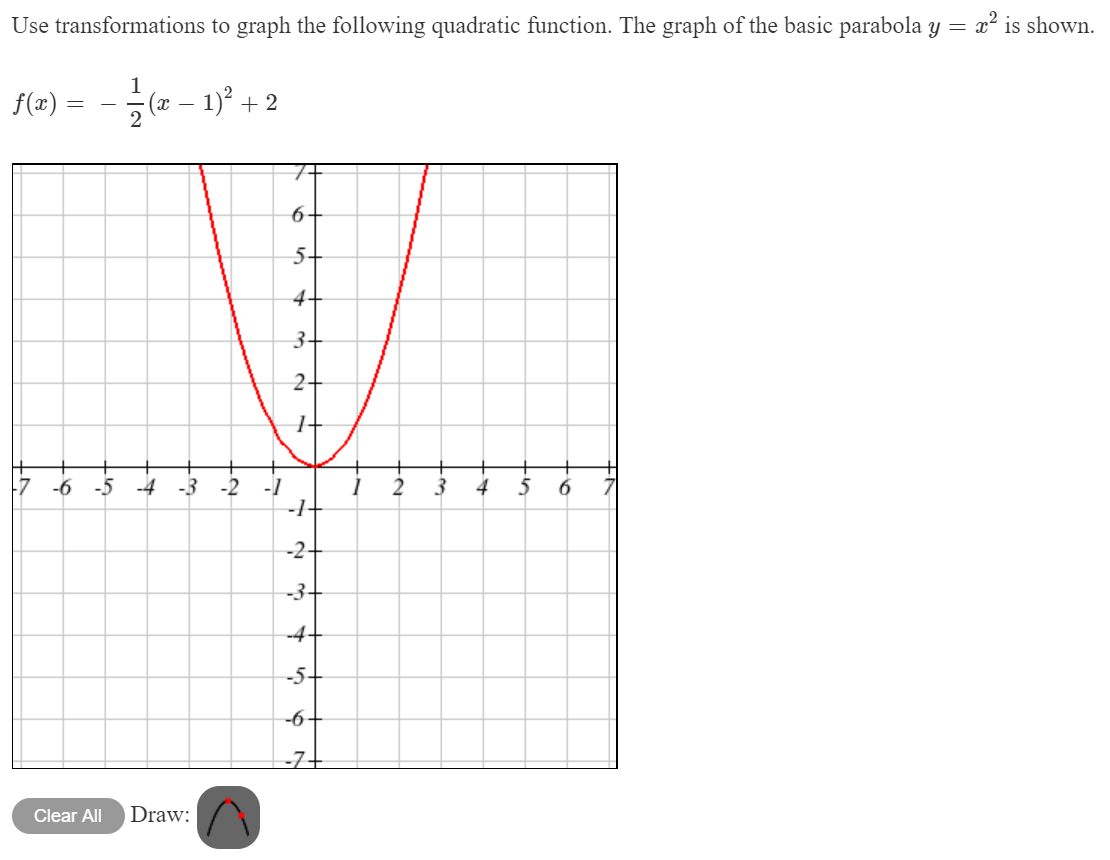
Solved Use Transformations To Graph The Following Quadratic Chegg Com

Have students predict what they think the graphs of y = sin(x 2) and y = sin(x 2) will look like y = sin(x 2) y = sin(x 2) Notice that in the graph of y = sin(x 2) the sine curve has been translated to the left two units In the graph of y = sin(x 2)2 For the following linear transformations T Rn!Rn, nd a matrix A such that T(~x) = A~x for all ~x 2Rn (a) T R2!R3, T x y = 2 4 x y 3y 4x 5y 3 5 Solution To gure out the matrix for a linear transformation from Rn, we nd the matrix A whose rst column is T(~e 1), whose second columnSection 12 Transformations of Linear and Absolute Value Functions 13 Writing Refl ections of Functions Let f(x) = ∣ x 3 ∣ 1 a Write a function g whose graph is a refl ection in the xaxis of the graph of f b Write a function h whose graph is a refl ection in the yaxis of the graph of f SOLUTION a A refl ection in the xaxis changes the sign of each output value

2

2

1) y = (x 3)2 Transformations reflected in the xaxis (flipped upside down) translated 3 units to the leftExample 2 Write the steps to obtain the graph of the function y = 3 (x − 1) 2 5 from the graph y = x 2 Solution Step 1 By graphing the curve y = x 2, we get a open upward parabola with vertex (0, 0) Step 2 Here 1 is subtracted from x, so we have to shift the graph of yDefine the rigid transformations and use them to sketch graphs Define the nonrigid transformations and use them to sketch graphs Vertical and Horizontal Translations When the graph of a function is changed in appearance and/or location we call it a transformation There are two types of transformations y = x 2 B a s i c

Using Transformations To Graph Functions

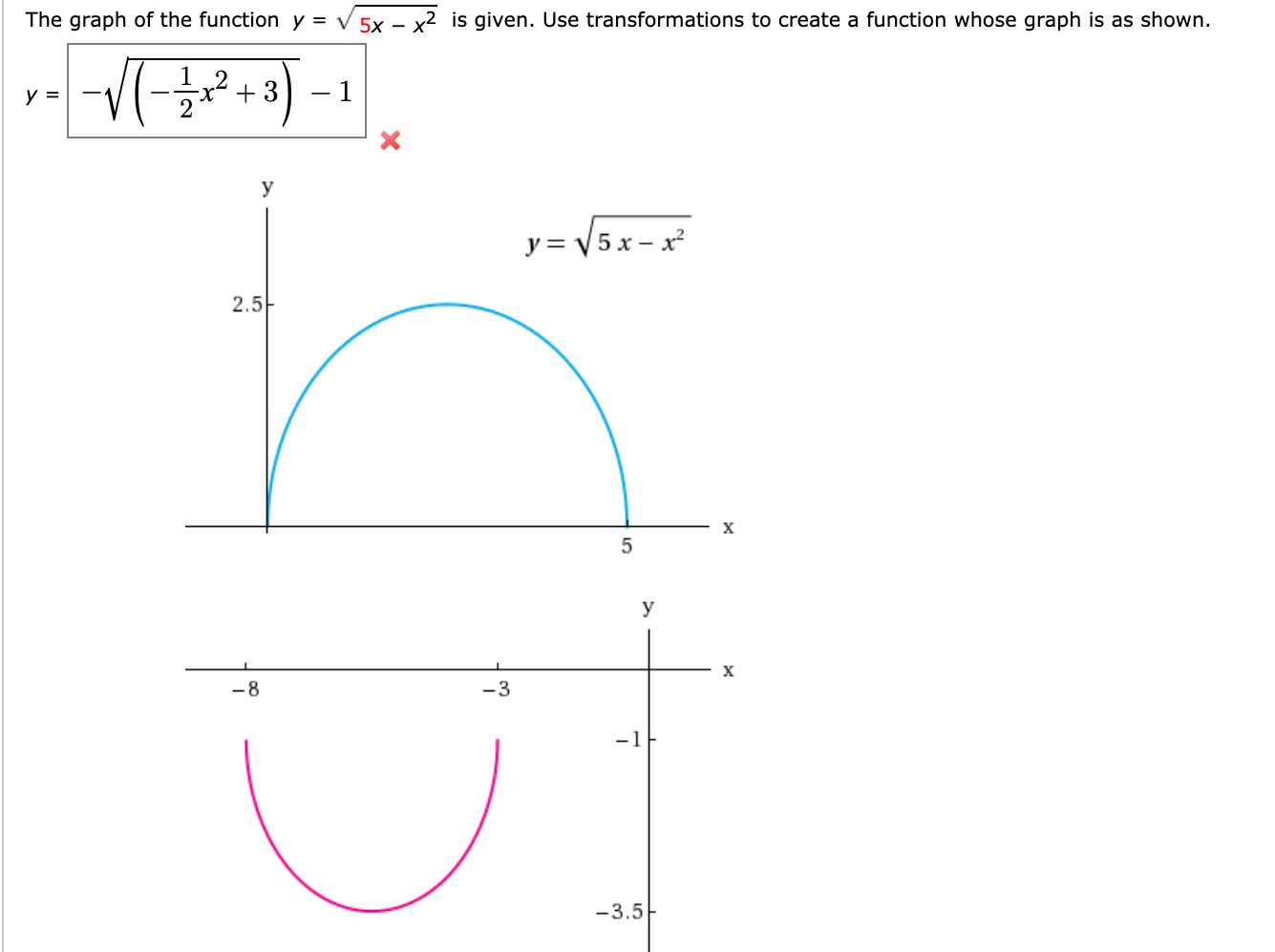
Solved The Graph Of The Function Y V 5x X2 Is Given Use Chegg Com

Transformations of Two Random Variables Problem (X;Y) is a bivariate rv Find the distribution of Z = g(X;Y) The very 1st step specify the support of ZQuestion 2 SURVEY 900 seconds Report an issue Q Identify the transformation from the graph of f (x)=x 2 to the graph g (x)= (x5) 2 answer choices shifted up five units reflection in xaxisUse transformations to graph y = 3x^2

Jdlogo Home Functions Defined Functions You Should Know Transformations Of Quadratics Translations Reflections Inverses Stretches Combinations Combining Functions Review Test Unit 2 Functions And Transformations Lesson 3a

Transformations Of Quadratic Functions College Algebra

15) The graph of y= x2 is on the left;Have a play with this 2D transformation app Matrices can also transform from 3D to 2D (very useful for computer graphics), do 3D transformations and much much more The Mathematics For each x,y point that makes up the shape we do this matrix multiplicationThis function is the image off(x) = x3 under the transformations defined by y Since h 2 and k —1, the function is then translated 2 units left and 1 unit down The image graph can be obtained by applying the mapping (x, y) — (x —2, y— 1) to the original points on the curve — 1

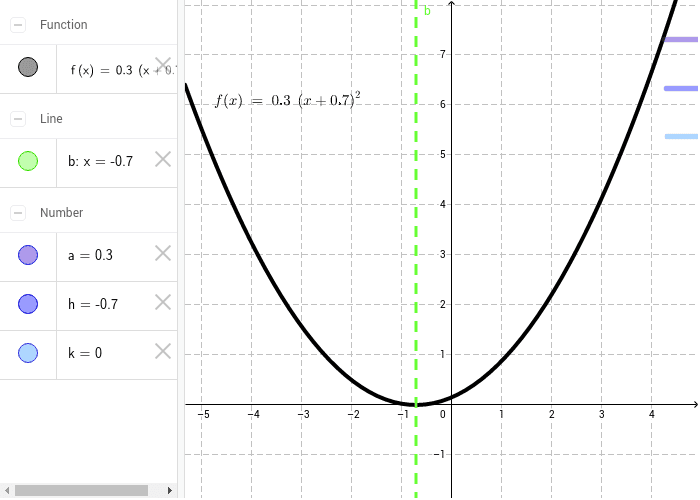
Transformations To The Graph Of Y X 2 Geogebra

This Graphical Representation Shows Transformations Associated With Y Download Scientific Diagram

Shift to the right by 2 units, vertical translation upwards by 3 units The parent function of the graph is y=x^2 Using the general equation y=af(kxd)c, Where if a >(a) Reflect in the yaxis, then shift left 2 units (b) Shift left 2 units, then reflect in the yaxis (c) Do parts (a) and (b) yield the same function?Transformations, part 2 Transformations, part 3 output and specifically it'll be f of X is equal to cosine of X cosine of X and then the Y component will be X sine of Y sorry X sine of X so just just to think about it examples if you plug in something like zero and think about where zero ought to go you would have F of zero is equal to

Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation

Transformations In Math Definition Graph Video Lesson Transcript Study Com

Y y= x y 2 4 6 8 10 x 224 4 0 step 3 vertical translation step 2 vertical reflection = 2x 3 Method 2 Use Mapping Notation Apply each transformation to the point (xy, ) to determine a general mapping notation for the transformed function Transformation of y= √ __ x Mapping Horizontal stretch by a factor of 1 _ (2 x, y) → (1 _x 2, yN(0;2¾2)† What is the joint distribution of U = X Y and V = X=Y if X »Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

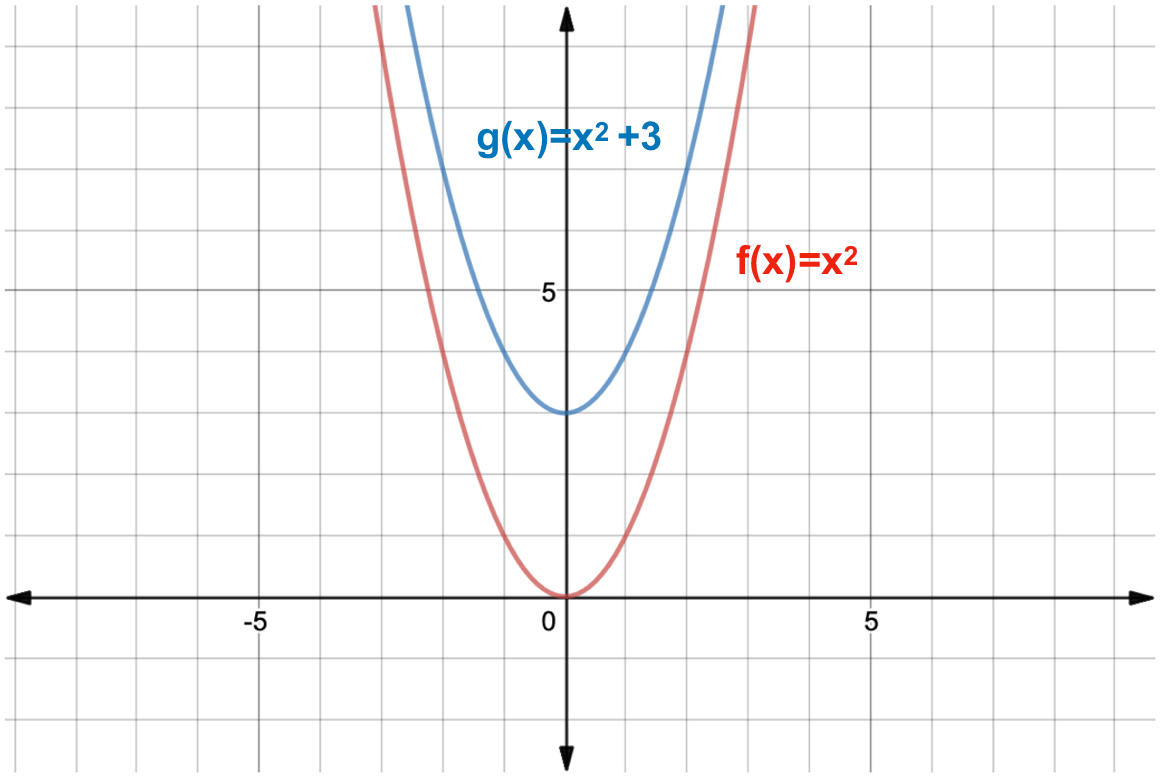
What Is A Function Transformation Expii

Content Geometric Transformations Of Graphs Of Functions

1= vertical compression f(x)=reflection in the xaxis f(x)=reflection in the yaxis 0 <VCE Maths Methods Unit 3 Transformation of functions y=x 32 Re!ections (in the x axis) 5 • Re!ections !ip the graph around the x or y axis • Re!ections keep the shape of the graph the same • A re!ection in the x axis signs are changed for y values (1,3)About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &

Graphing With Transformations Quantitative Reasoning

Solution Graph The Function F By Starting With The Graph Of Y X2 And Using Transformations Shifting Compressing Stretching And Or Reflection Hint If Necessary Write F In The

C(0;1){V = X ¡Y »But you can't see it, because x 2 is symmetrical about the yaxis So here is another example using √(x) g(x) = √(−x) This is also called reflection about the yIn general, transformations in ydirection are easier than transformations in xdirection, see below How to move a function in ydirection?

5 Pre Assessment Transformations Of Functions

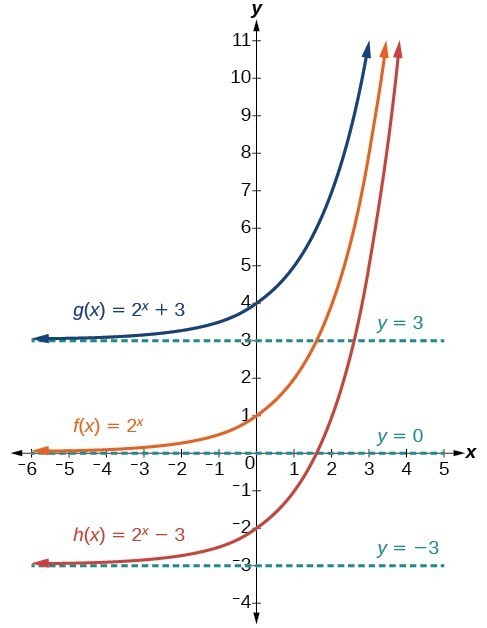
Graph Exponential Functions Using Transformations College Algebra

Transformations and Matrices A matrix can do geometric transformations!The graph of \(f(x) = x^2\) is the same as the graph of \(y = x^2\) Writing graphs as functions in the form \(f(x)\) is useful when applying translations and reflections to graphs TranslationsY = 2x y = 2 x The transformation from the first equation to the second one can be found by finding a a, h h, and k k for each equation y = abx−h k y = a b x h k Find a a, h h, and k k for f (x) = 2x f ( x) = 2 x a = 1 a = 1 h = 0 h = 0 k = 0 k = 0 The horizontal shift depends on

Transformations Of Y X2 In Vertex Form Organizer And Presentation

Function Transformations

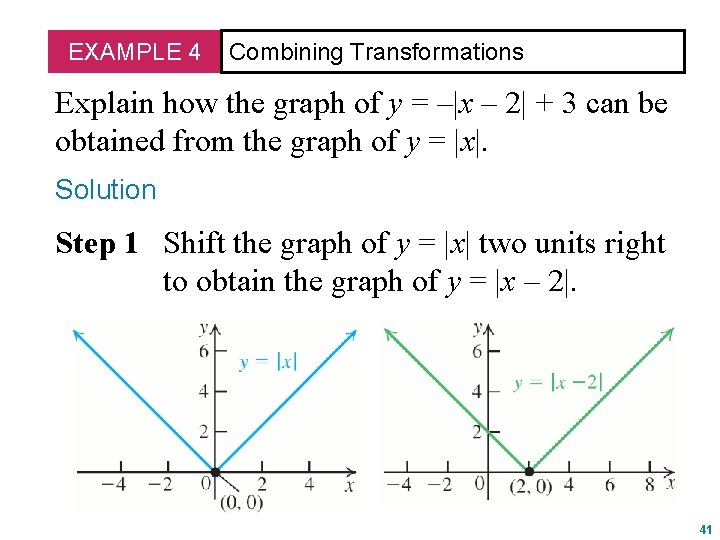
Graph transformation is the process by which an existing graph, or graphed equation, is modified to produce a variation of the proceeding graph It's a common type of problem in algebra, specifically the modification of algebraic equations Sometimes graphsPoint Z is located at $$ (2,3) $$ , what are the coordinates of its image $$ Z'$$ after a reflection over the xaxis Show Answer Remember to reflect over the xaxis ,Safety How works Test new features Press Copyright Contact us Creators

Transformations Of Section Functions 2 7 2 Learn

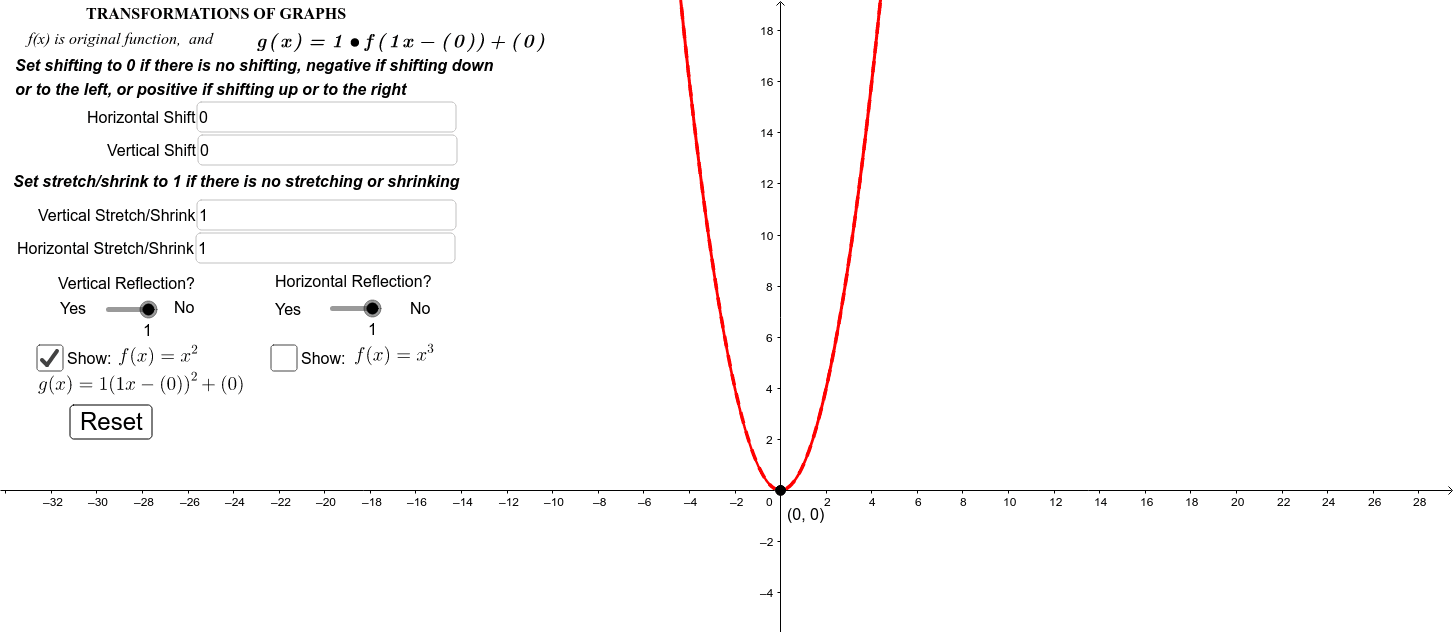
Transformation Of Y X 2 And Y X 3 Geogebra

We can flip it leftright by multiplying the xvalue by −1 g(x) = (−x) 2 It really does flip it left and right!Y=X^2 Transformations Y=X^2 Transformations Log InorSign Up y = a bx − h 2 k 1 h = 0 2 k = 0 3 a = 1 4 b =Now consider a transformation of X in the form Y = 2X2 X There are five possible outcomes for Y, ie, 0, 3, 10, 21, 36 Given that the function is onetoone, we can make up a table describing the probability distribution for Y TABLE 3 ProbabilityofaFunction oftheNumberofHeadsfromTossing aCoin Four Times Y = 2 * (# heads)2 # of heads

1

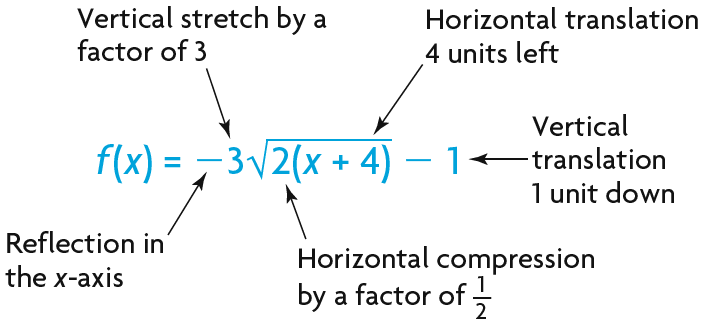
Using Transformations To Graph Functions Of The Form

Q The coordinates of triangle JRB are ,J(1, 2) , R(3, 6) and B(4, 5) What are the coordinates of the vertices of its image after the transformation (x, y)→(x2, y1) and reflect across the y axis?In order to graph the function {eq}f(x)=(x2)^2 {/eq}, we need to translate the graph of the parent function by 2 units to the left Note that adding a units in the xvariable means translatingThe graph of y= 3(x 5)2 7 is on the right If one looks carefully, one can see that the labels on the yaxis have changed, otherwise the graphs are the same Figure 13 Graphs of y= x2 and y= 3(x 5)2 7 (Generated by the author using Sage) There are four types of transformations we will study in this

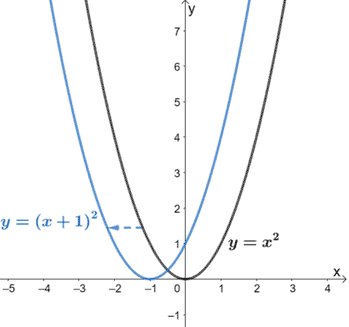
Transformations Of Functions Explanation Examples

Transformations Of Functions Ck 12 Foundation

Two Examples of Linear Transformations (1) Diagonal Matrices A diagonal matrix is a matrix of the form D= 2 6 6 6 4 d 1 0 0 0 d 2 0 0 0 0 d n 3 7 7 7 5 The linear transformation de ned by Dhas the following e ect Vectors areTransformations are the key to graphing and explaining where the parabola is It is only used in vertex form because each letter except x and y represents a transformation in this equation y=a(xh)^2k h = the vertex of the parabola will move to the right or left side of the graph1¾2) {U = X=Y »

The Graph Of The Function Y Sqrt 3x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Study Com

Transformations Of Y X Ck 12 Foundation

1= horizontal compression d=horizontal shift to the right d=Start studying Transformation Rules (x,y)>The above movement is a demonstration of a translation, the image is remaining the same size just moving positions on the graph In the above graph point A is moved from (0, 0) to (5, 2) at A', therefore, the translation being shown is an up 2 units and to the right five units, which can be shown as (x 5, y 2)

1 07 Transformations Of Functions

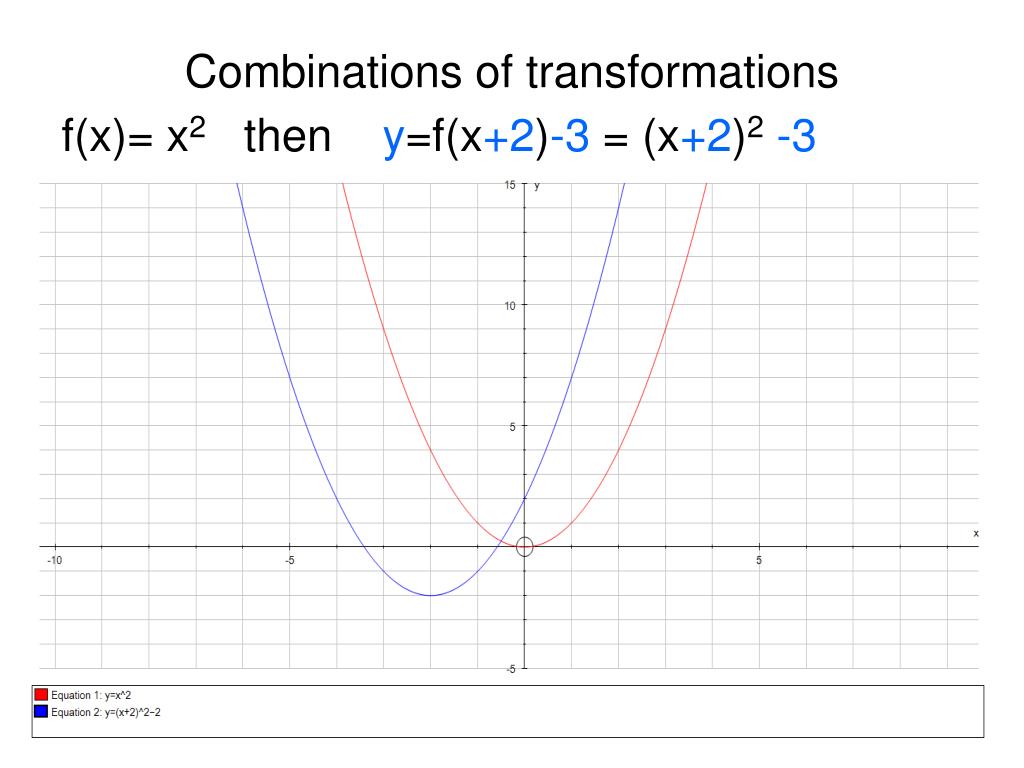
最も選択された Yx2 Transformations シモネタ

See below The first thing you need to find is the axis of symmetry by using b/2a after you find that, use it to find the vertex of x^28 In this case x should equal 0 so y=0^28 giving just 8 the yintercept is 8 as c=8 the graph should look like this graph{x^28 115, 85, 084, 1084} it is a parabola

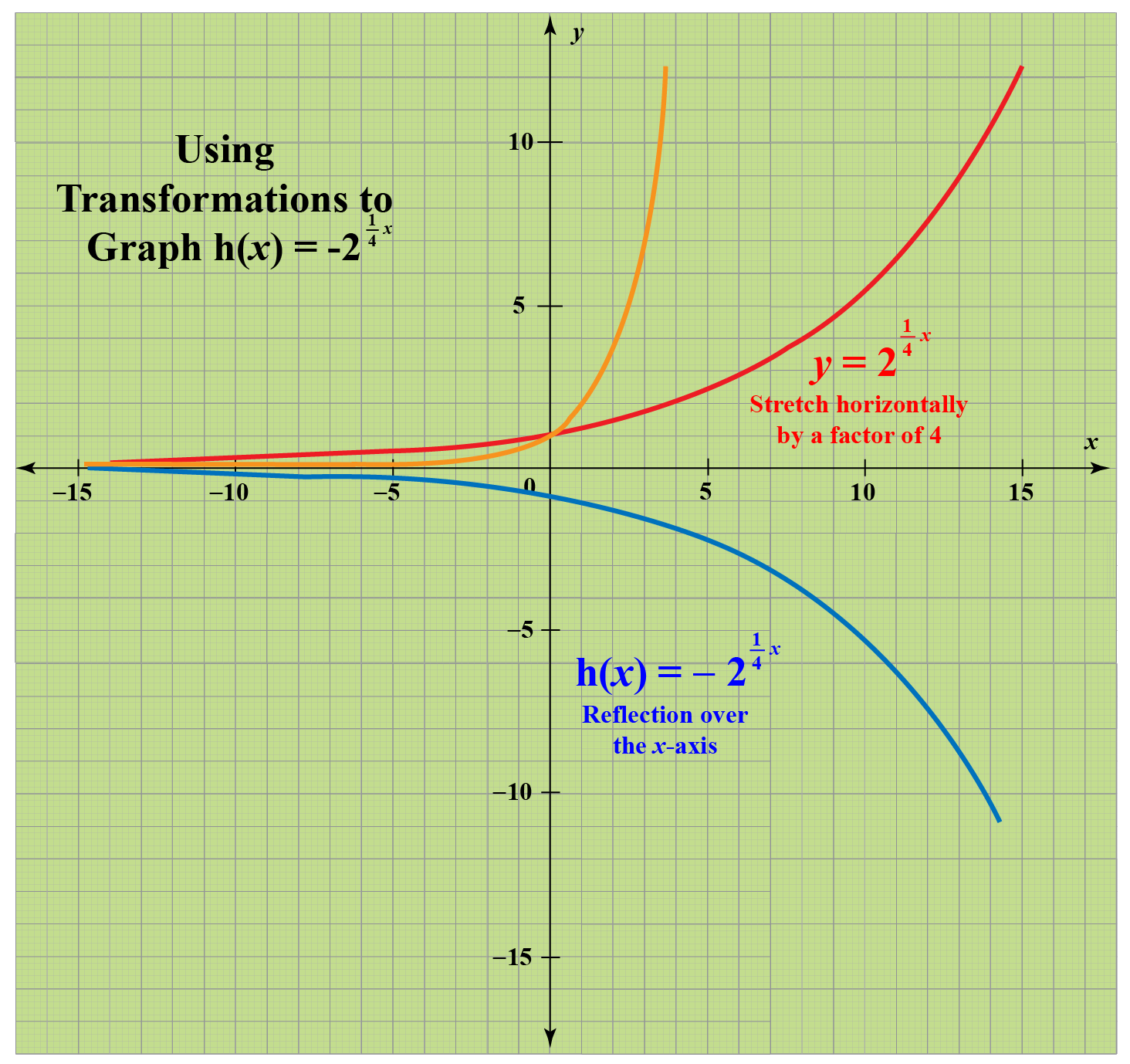
Transformations Of Functions Definitions Facts And Solved Examples Cuemath

The Parabola Y X2 Has Been Transformed Into Y 2 X 1 2 6 What Are All The Transformations Quora

Functions Transformations Isaac Physics

Which Type Of Transformation Is Described By X Y X 2 Y 3 Brainly Com

Solution How Do These Transformations Change The Graph Of F X Combining Functions Underground Mathematics

1

K

Using Transformations To Graph Functions

Content Transformations Of The Parabola

Discovering Advanced Algebra Resources

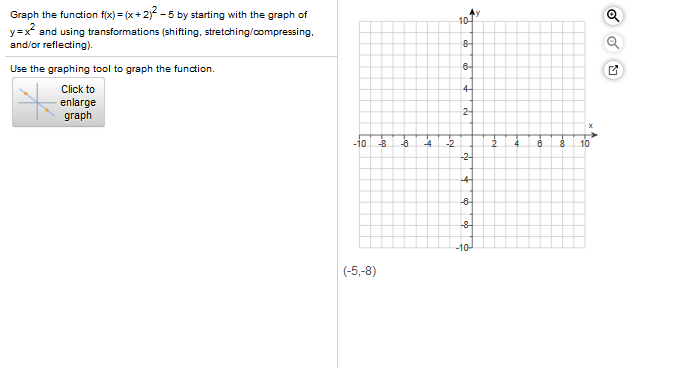
Solved Graph The Function F X X 1 2 4 By Starting Chegg Com

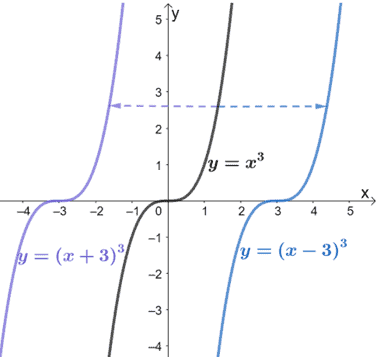
Transformations Of Functions Explanation Examples

Parabola Transformations Zona Land Education

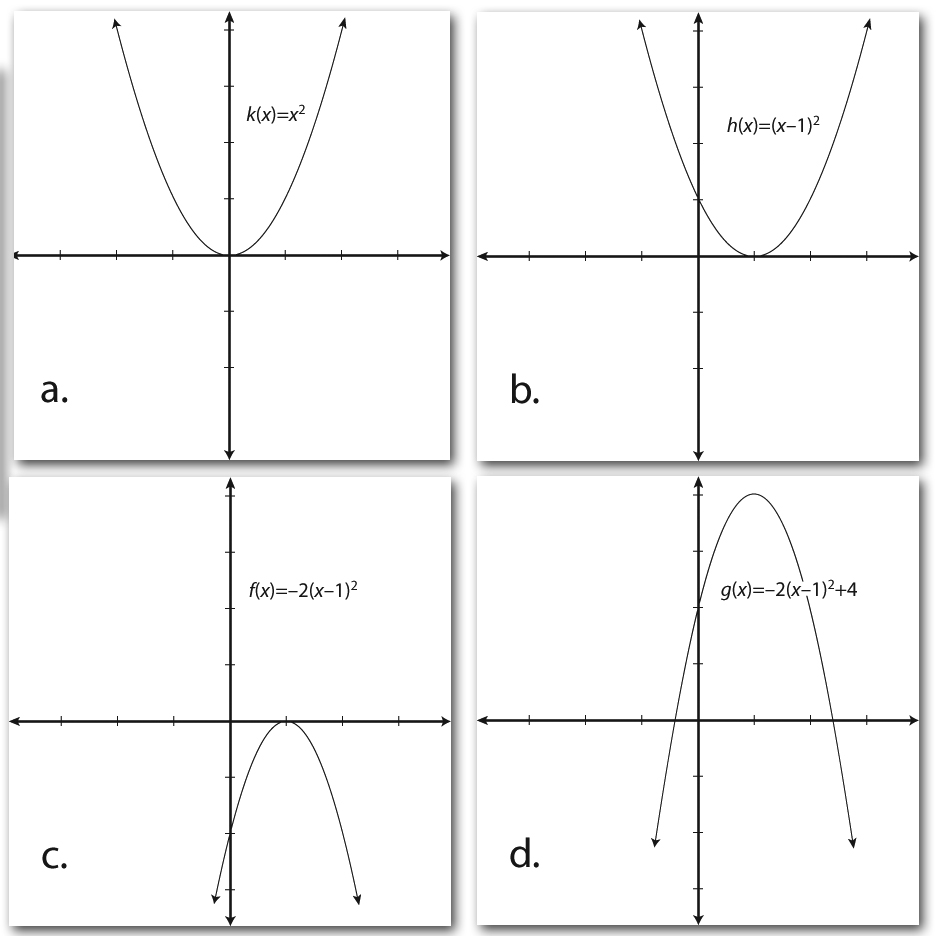
How To Combine Various Transformations Dummies

Transformation Of Graphs Highschool Learnmath

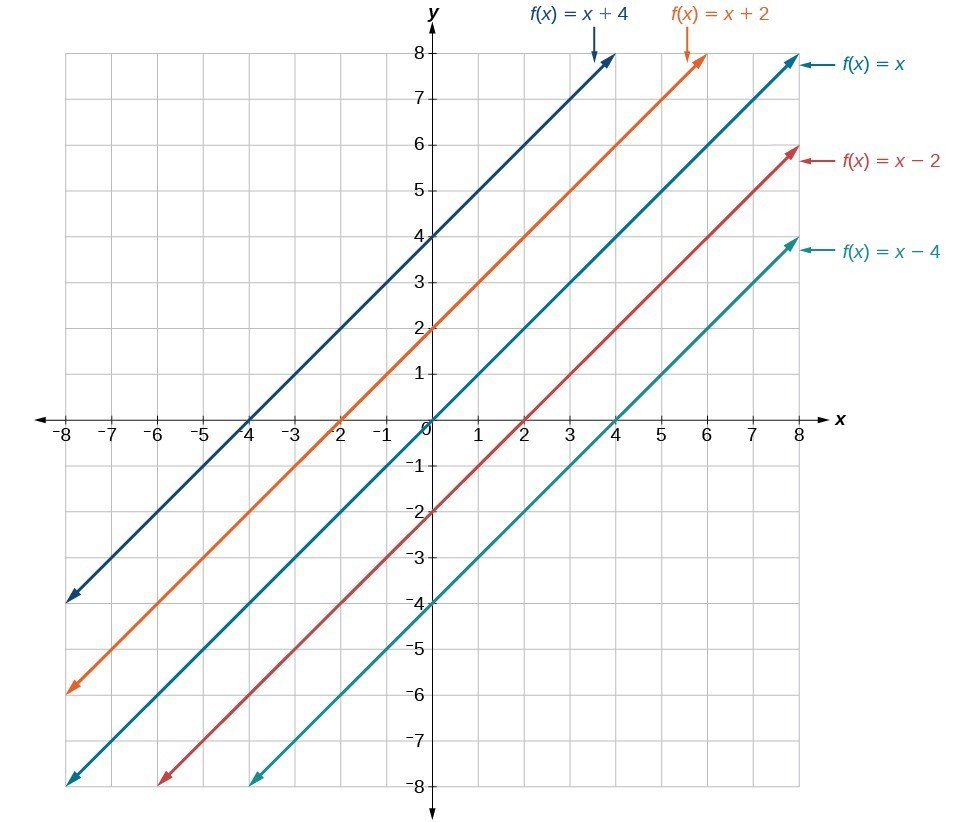
Read Transform Linear Functions Intermediate Algebra

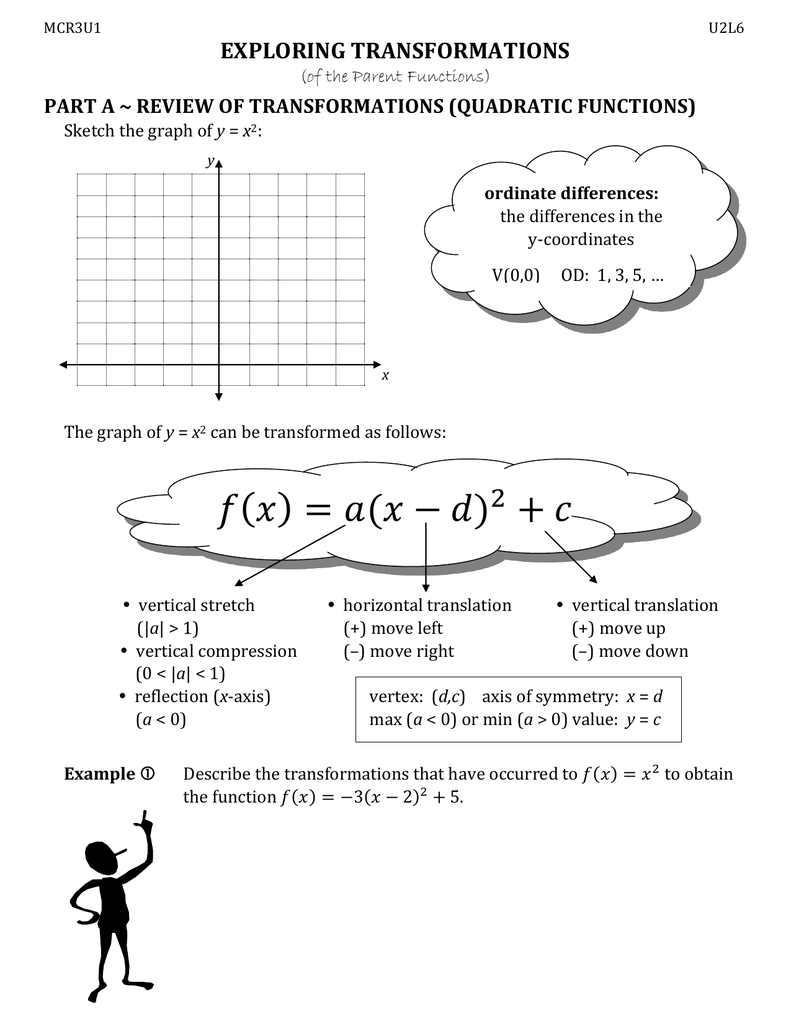
Exploring Transformations Of Parent Functions

Solution Describe The Transformation From The Parent Function Y X 6 Y 2 X 5 6 3

Transformations Mrs F X

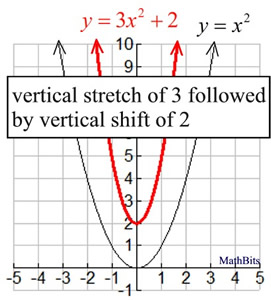
Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math

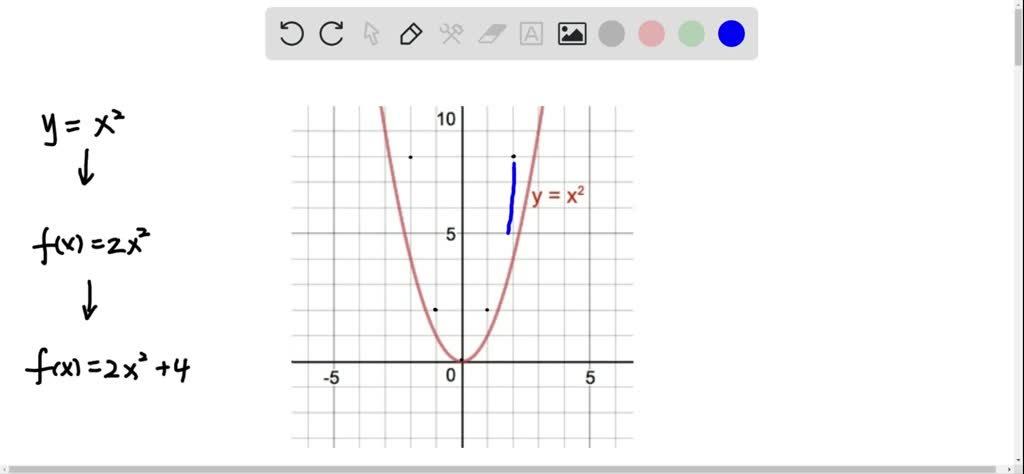
Solved Graph The Function F By Starting With The Graph Of Y X 2 And Using Transformations F X 2 X 2 4

How Do You Sketch The Graph Of Y X 2 2x And Describe The Transformation Socratic

2

1

Algebra 2 Transformations Of Parent Functions Youtube

Transformations Of Graphs

Symmetry Transformations And Compositions

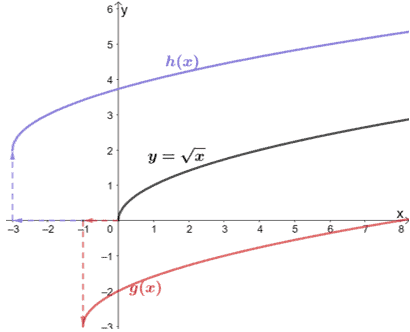
Transformations Of Functions Explanation Examples

2

Transformations

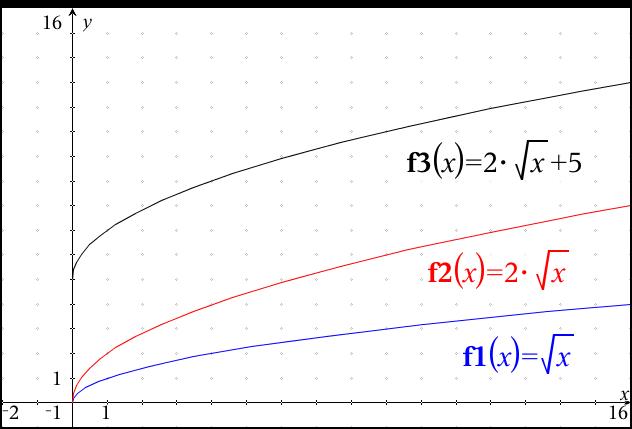
How Do You Identify Transformations In Parent Functions Given Y 2sqrtx 5 Socratic

Content Transformations Of The Parabola

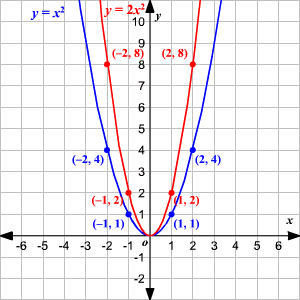
Graphing Quadratic Equations Using Transformations

The Function Y X 4 2 3 Is A Transformation Of The Function Y X How Is The Function S Brainly Com

Sec 2 4 Transformation Of Graphs Copyright C By Houghton Mifflin Company Inc All Rights Reserved 2 The Graphs Of Many Functions Are Transformations Ppt Download

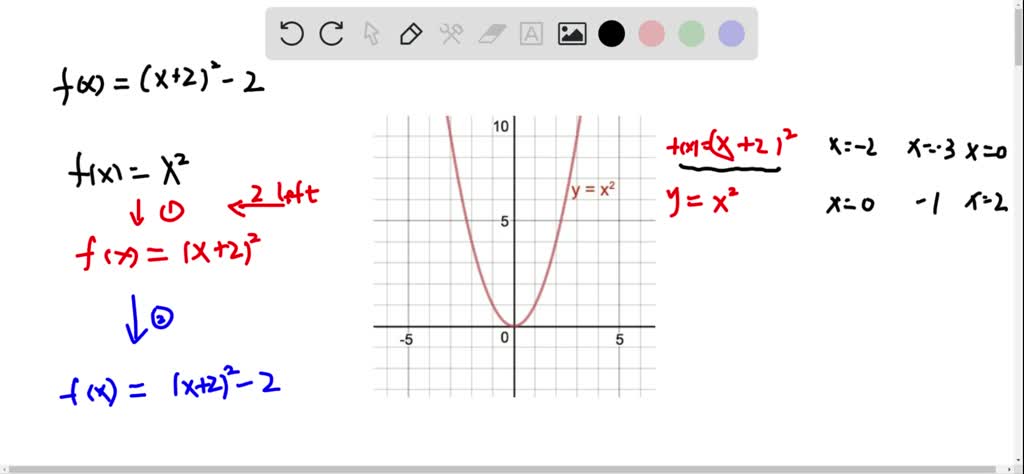
Solved Graph The Function F X X 1 2 2 By Starting With The Graph Of Y X 2 And Using Transformations Shifting Stretching Compressing And Or Reflecting

Transformations Left Or Right

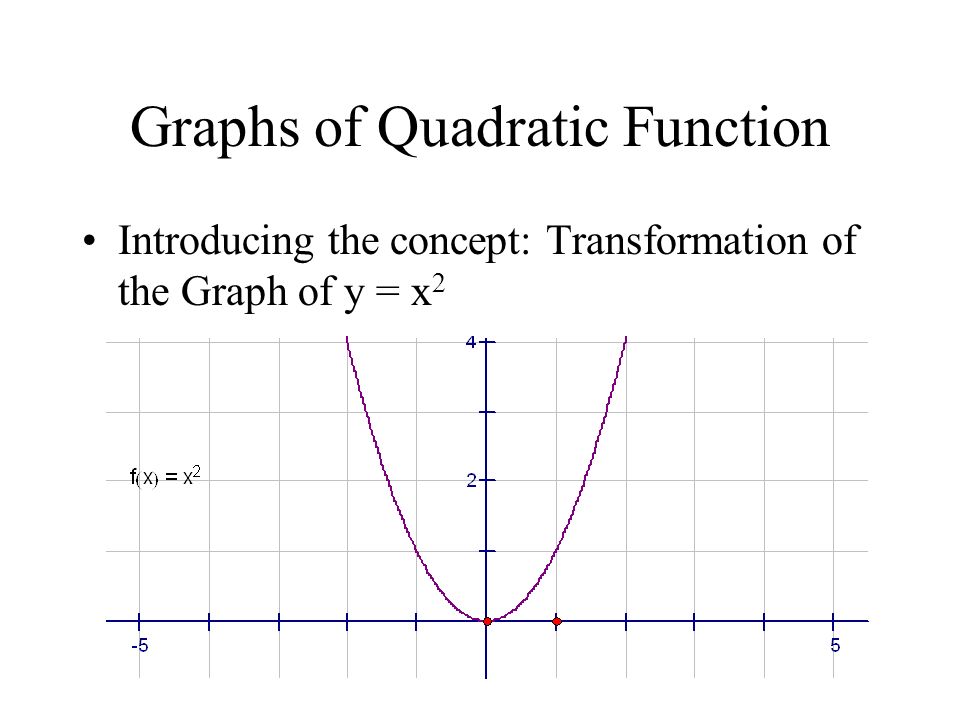
Graphs Of Quadratic Function Introducing The Concept Transformation Of The Graph Of Y X Ppt Download

Quadratic Transformations Part 2 Activity Builder By Desmos

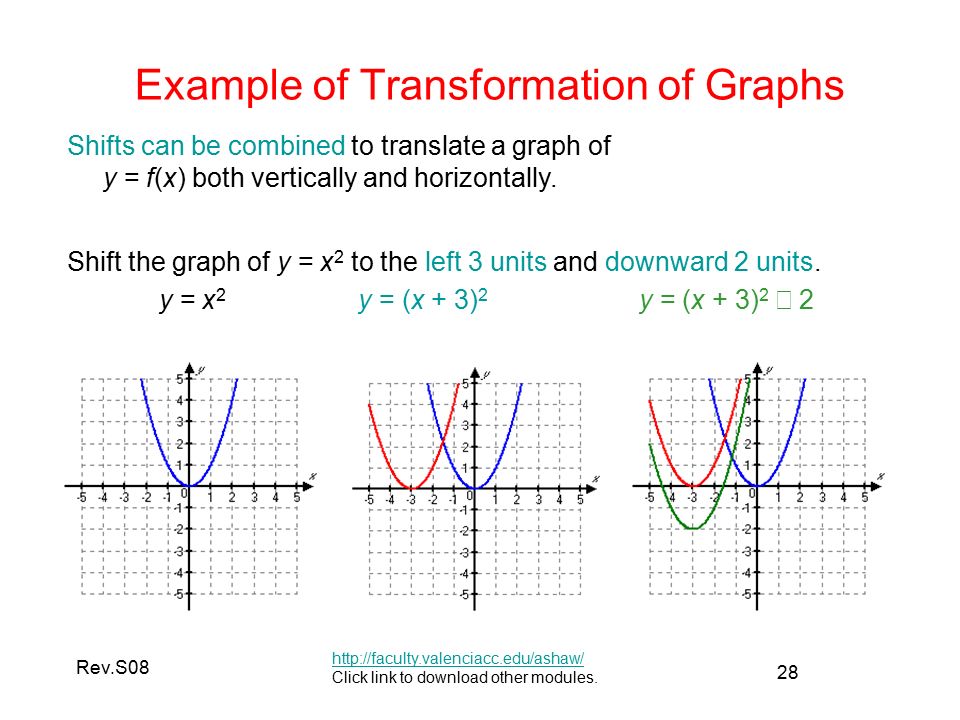
Transformation Of Graphs Ppt Video Online Download

Stretch Or Compress Function Vertically Cf X Expii

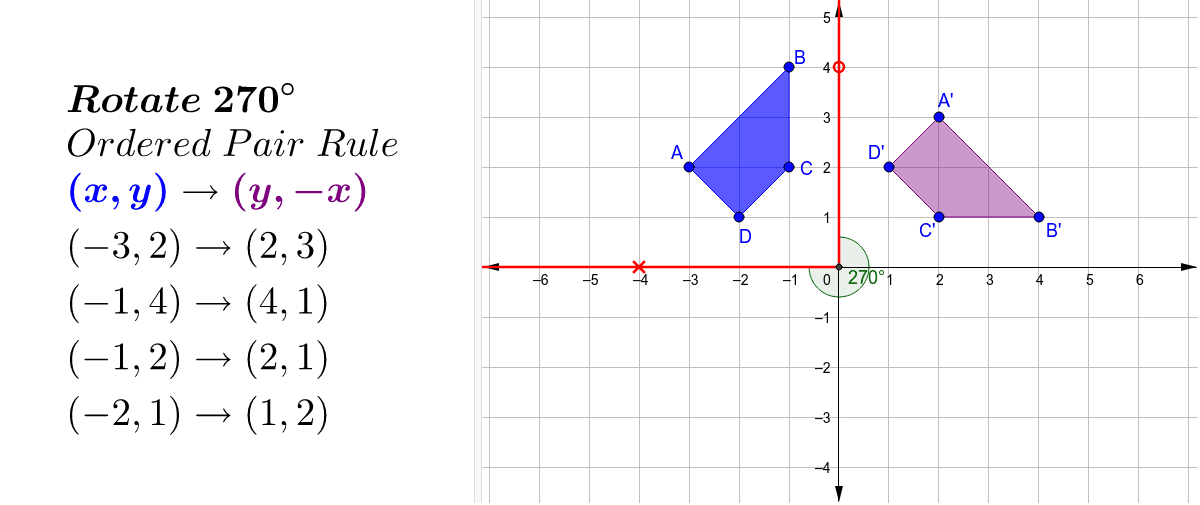
Transformation Y X Geogebra

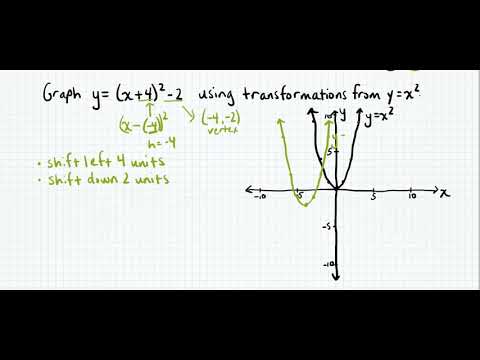
Graphing Transformations Of Y X 2 Youtube

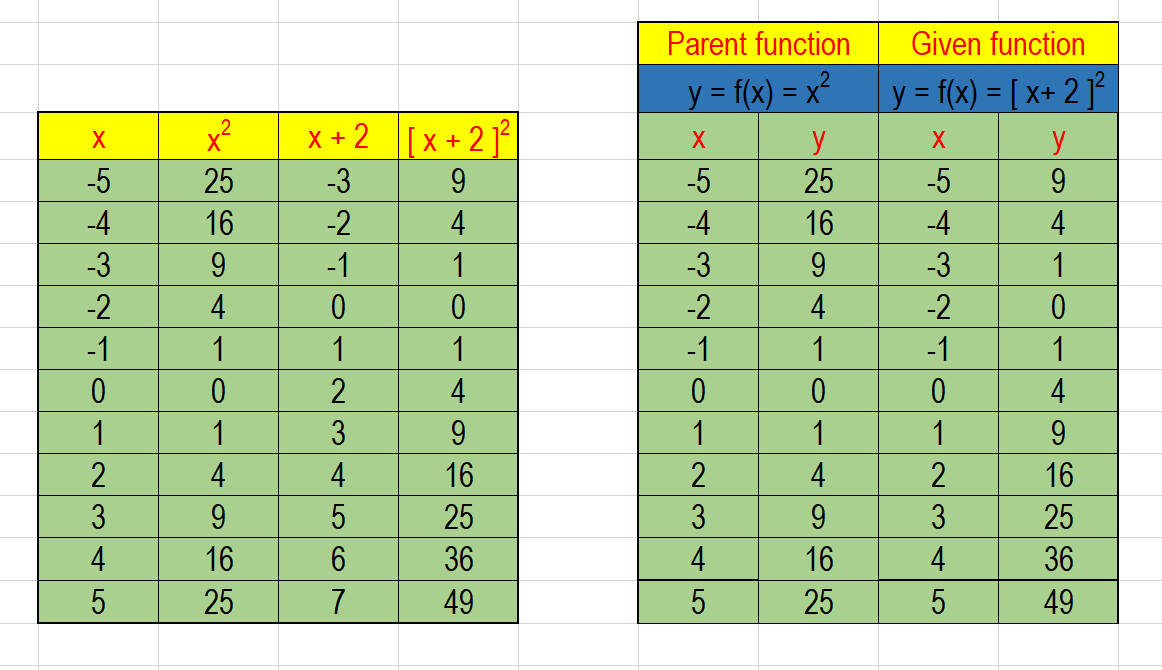
How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic

The Graph Of Y Sqrt 4x X 2 Is Given Below Use Transformations To Create A Function Whose Graph Is As Shown Below Study Com

Combining Transformations Ck 12 Foundation

Graph Transformations Muic Math

Content Transformations Of The Parabola

Absolute Value Transformations

Solution I Have A Question That States A Use The Transformations On The Graph Of Y X 2 To Determine The Graph Of Y X 5 2 9 B Using The Graph Of F X X 2 As A Guide Graph

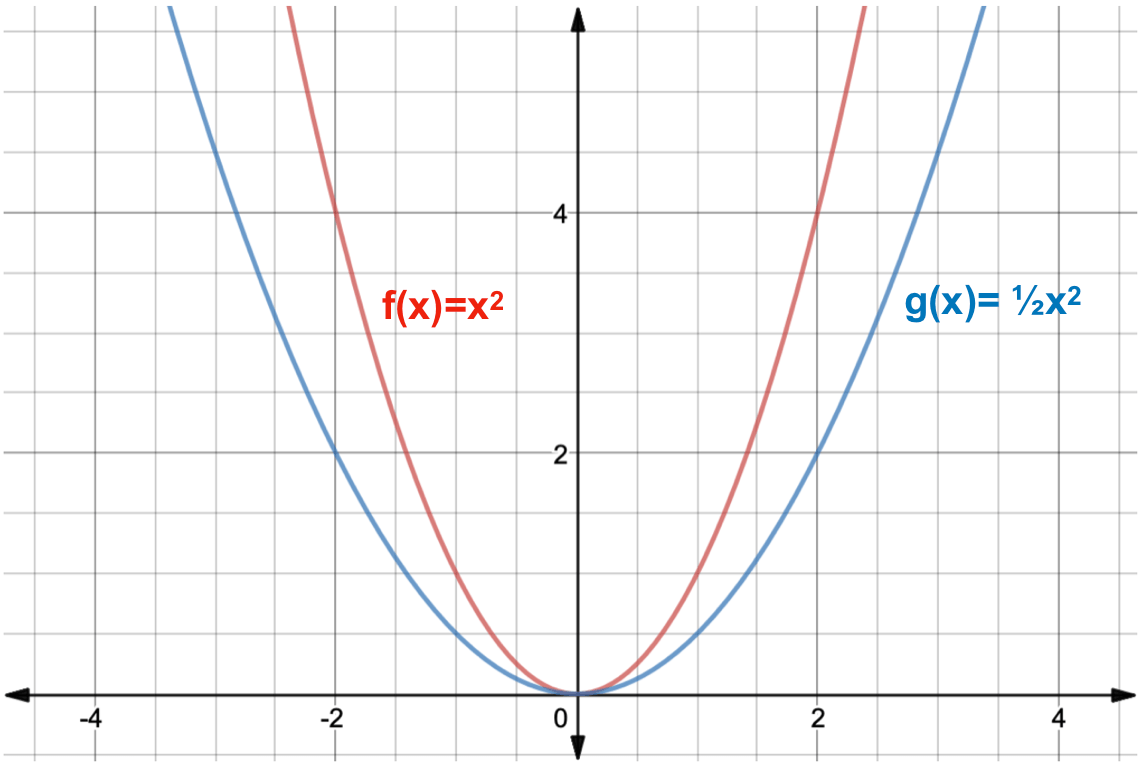
What Is A Function Transformation Expii

Transformations Bingo Card

Solved Graph The Function F By Starting With The Graph Of Chegg Com

Y X 2

What Transformations Are Needed To Transform The Graph Of The Parabola Y X 2 Into The Graph Of The Parabola Y X 2 4x 6 Quora

Trasformations By Graph Paper Teacher Guide

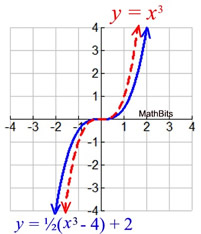
Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math

Solved Match The Rule With The Transformation Y X 2 X Y 3 Y X 4 X Y 5 X 3 Y 5 6 Y X 7 X Y 8 Y X 9 Course Hero

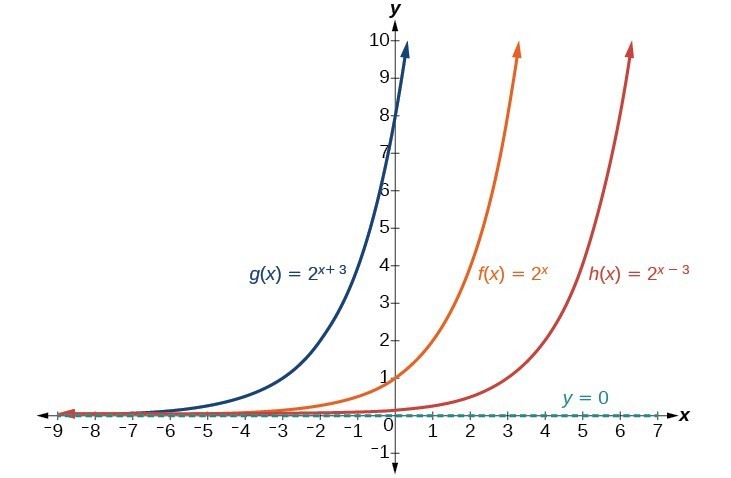
Graph Exponential Functions Using Transformations College Algebra

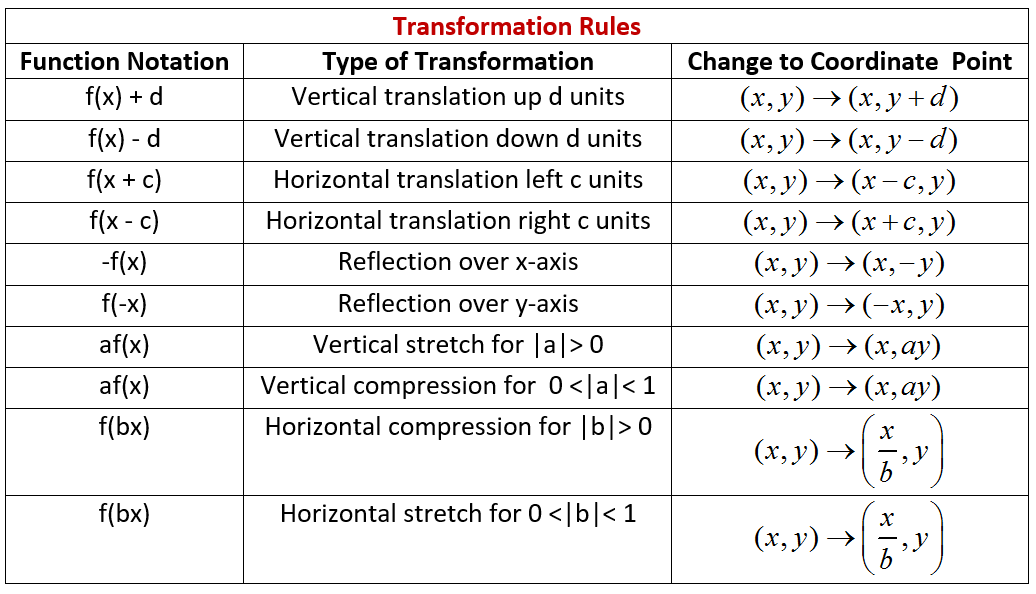
How Do You Sketch The Graph Of Y X 2 2 2 And Describe The Transformation Socratic

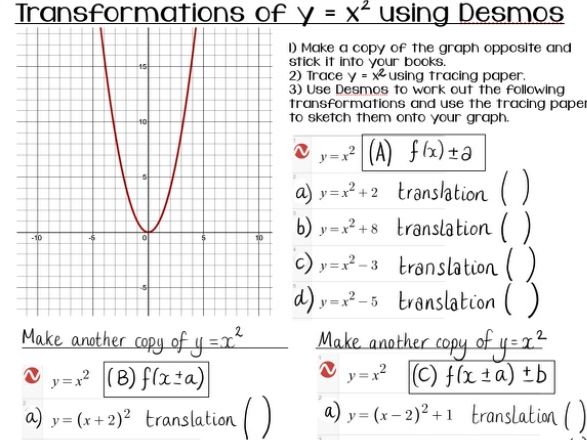
Transformations Of Y X 2 Using Desmos Teaching Resources

Transformations Up Or Down

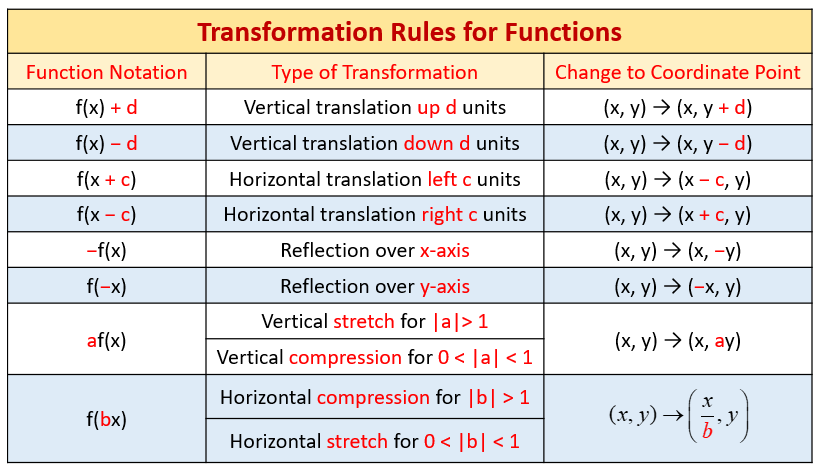
Parent Functions And Their Graphs Video Lessons Examples And Solutions

Vce School Notes Graph Transformations

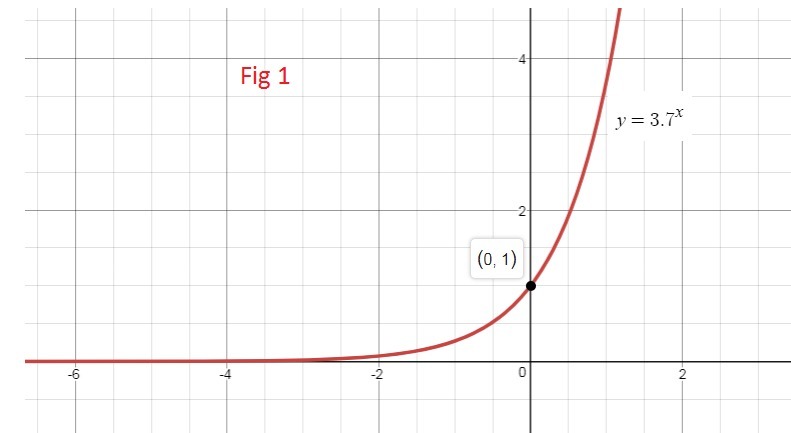
How Can You Use Transformations To Graph This Function Y 3 7 X 2 Explain Your Steps

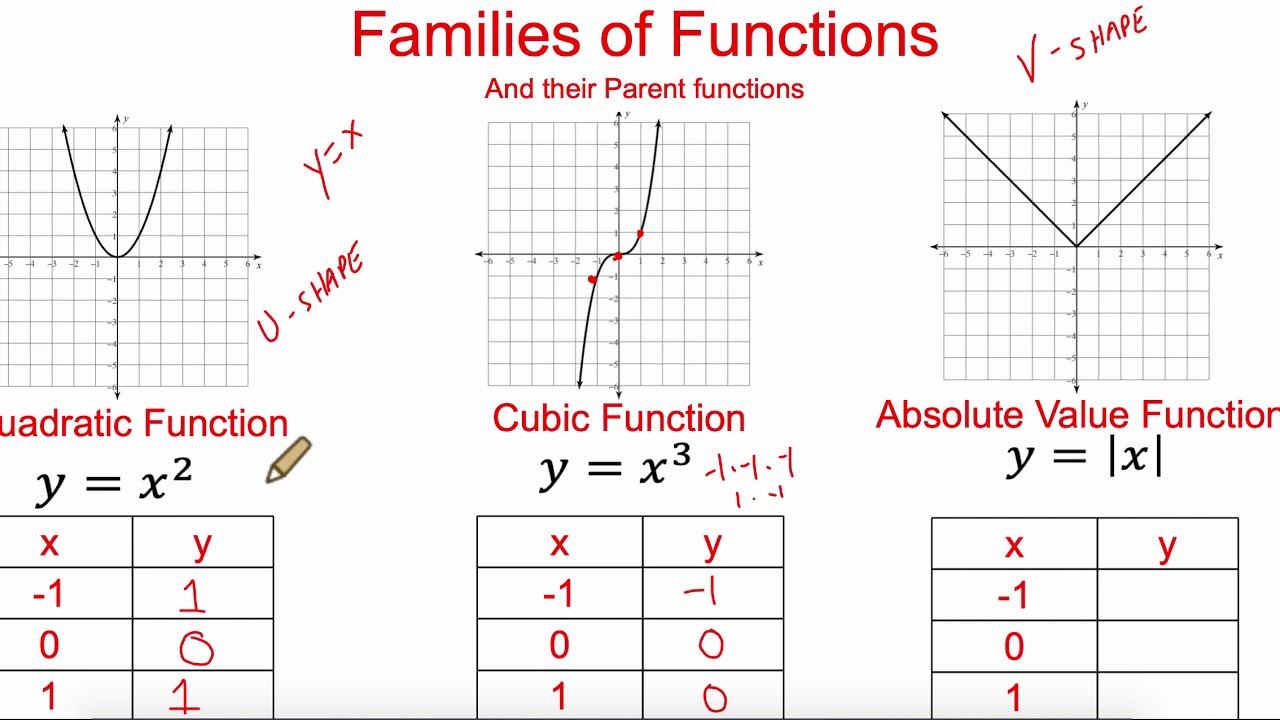
Algebra 2 Transformations Of Functions Pt 1 Youtube

3 5 Transformations Of Graphs Graph Functions Using

Grade 10 Transformations Of Y X 2 Youtube

Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation

Reflecting Functions Examples Video Khan Academy

Incoming Term: y x 2 transformation, transformations of y x 2, transformations from y x 2,